Download this notebook from github.
Ensemble-Reduction Techniques
xclim.ensembles provides means of reducing the number of candidates in a sample to get a reasonable and representative spread of outcomes using a reduced number of candidates. By reducing the number of realizations in a strategic manner, we can significantly reduce the number of realizations to examine, while maintaining a statistical representation of the original dataset. This is particularly useful when computation power or time is a factor.
For more information on the principles and methods behind ensemble reduction techniques, see: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0152495 and https://doi.org/10.1175/JCLI-D-14-00636.1
[2]:
[2]:
<xarray.Dataset> Size: 2kB
Dimensions: (horizon: 2, realization: 50)
Coordinates:
* horizon (horizon) <U9 72B '2041-2070' '2071-2100'
Dimensions without coordinates: realization
Data variables:
delta_annual_tavg (horizon, realization) float64 800B 5.646 3.6 ... 6.144
delta_annual_prtot (horizon, realization) float64 800B 14.42 ... 20.69
delta_JJA_prtot (horizon, realization) float64 800B -1.108 ... 3.48[3]:
plt.style.use("seaborn-v0_8-dark")
plt.rcParams["figure.figsize"] = (13, 5)
fig = plt.figure(figsize=(11, 9))
ax = plt.axes(projection="3d")
for h in ds_crit.horizon:
ax.scatter(
ds_crit.sel(horizon=h).delta_annual_tavg,
ds_crit.sel(horizon=h).delta_annual_prtot,
ds_crit.sel(horizon=h).delta_JJA_prtot,
label=f"delta {h.values}",
)
ax.set_xlabel("delta_annual_tavg (C)")
ax.set_ylabel("delta_annual_prtot (%)")
ax.set_zlabel("delta_JJA_prtot (%)")
plt.legend()
plt.show()
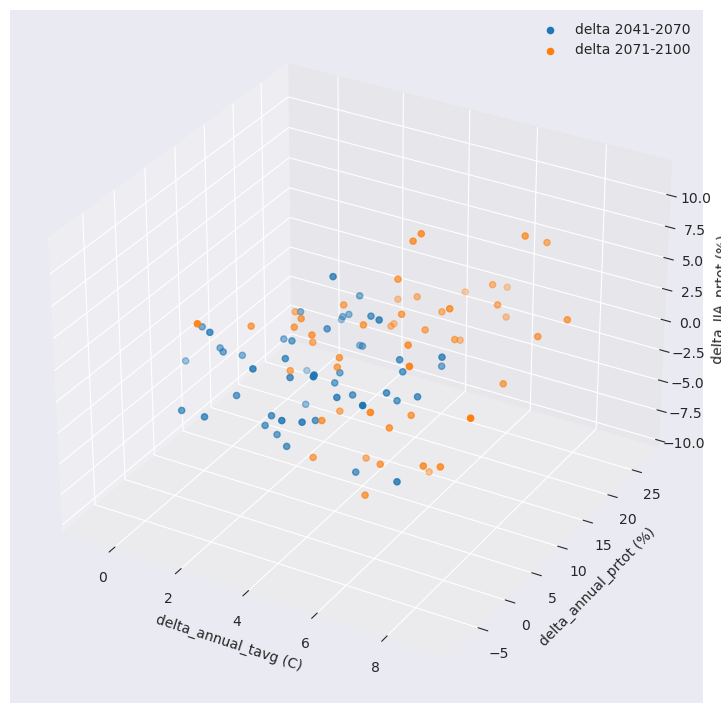
Ensemble reduction techniques in xclim require a 2D array with dimensions of criteria (values) and realization (runs/simulations). Hopefully, xclim has a function for this.
[4]:
crit = ensembles.make_criteria(ds_crit)
crit
[4]:
<xarray.DataArray 'criteria' (realization: 50, criteria: 6)> Size: 2kB
array([[ 5.64607852e+00, 3.54906688e+00, 1.44157535e+01,
9.45406716e+00, -1.10754551e+00, 4.08425951e+00],
[ 3.60023581e+00, 6.11380500e+00, -1.73879531e+00,
2.37067418e+01, -7.18137533e-01, -3.03151879e-01],
[ 4.46810698e+00, 4.31838972e+00, -1.35242499e+00,
4.04196142e+00, 3.29897879e+00, 2.56781265e+00],
[ 6.36133980e+00, 2.97873563e+00, 9.84698354e+00,
3.38849169e+00, 1.96579119e+00, 7.22686331e-01],
[ 5.80133699e+00, 5.28363554e+00, -8.65617026e-01,
9.21237980e+00, 1.92039458e+00, 4.76615500e+00],
[ 1.53408318e+00, 6.19666374e+00, 1.47181059e+01,
4.69217371e+00, -4.85086813e+00, 4.77899657e+00],
[ 4.42513263e+00, 5.47303444e+00, 2.93190510e+00,
1.90130874e+01, -7.29783732e-02, -9.02389514e-01],
[ 2.77296419e+00, 5.94494380e+00, 1.26272594e+00,
1.36054793e+00, -2.21409273e+00, -3.53345582e+00],
[ 2.84517172e+00, 4.07135581e+00, 1.46147101e+01,
8.20250781e-01, 8.39773797e-01, -4.33175359e+00],
[ 3.61589775e+00, 4.61451767e+00, 1.24025740e+01,
6.49743964e+00, -2.94451169e-01, 4.44151752e+00],
...
[ 1.42717055e+00, 4.53364611e+00, -2.45628796e+00,
-3.42855278e-01, -1.91231108e+00, -5.12350239e-01],
[ 8.69973094e-01, 7.78489014e+00, 7.19695851e+00,
1.21364070e+01, -1.19181544e+00, 7.58915262e-02],
[ 4.40594714e-01, 5.75654996e+00, 5.83336748e+00,
9.68573745e+00, -3.98641733e-01, 1.12156668e+01],
[ 5.92616309e+00, 7.29327807e+00, 8.17515718e+00,
6.55252018e-01, -8.93372638e-01, -2.24006329e+00],
[ 2.23552173e+00, 6.05273279e+00, 1.69157239e+01,
1.41862133e+01, -9.27038907e-01, 1.45620120e+00],
[ 2.34288855e+00, 6.75314634e+00, 9.72239743e+00,
8.62762935e+00, -5.02801142e+00, 6.54756545e+00],
[ 1.12080696e+00, 5.36100004e+00, 4.35888873e-01,
1.61743244e+01, 3.45699469e+00, 2.39089987e+00],
[ 4.16623553e+00, 8.91174099e+00, 1.05850814e+01,
1.65880332e+01, 3.23885578e+00, 4.33181472e+00],
[ 5.79153229e-01, 5.59382419e+00, -1.57953705e+00,
2.73058876e+01, -2.44009278e+00, 4.02203883e-01],
[ 2.68088958e+00, 6.14397873e+00, 2.69207698e+00,
2.06922236e+01, -4.39927298e+00, 3.48022355e+00]])
Coordinates:
* criteria (criteria) object 48B MultiIndex
* horizon (criteria) object 48B '2041-2070' '2071-2100' ... '2071-2100'
* variables (criteria) object 48B 'delta_annual_tavg' ... 'delta_JJA_prtot'
Dimensions without coordinates: realizationK-Means reduce ensemble
The kmeans_reduce_ensemble works by grouping realizations into subgroups based on the provided criteria and retaining a representative realization per subgroup.
For a real-world example of the K-means clustering algorithm applied to climate data selection, see: https://doi.org/10.1371/journal.pone.0152495 and https://doi.org/10.1175/JCLI-D-11-00440.1
The following example uses method = dict(n_clusters=25) in order to take the original 50 realizations and reduce them down to 25. The function itself returns the ids (indexes: int) of the realizations, which can then be used to select the data from the original ensemble.
[5]:
ids, cluster, fig_data = ensembles.kmeans_reduce_ensemble(
data=crit, method={"n_clusters": 25}, random_state=42, make_graph=True
)
ds_crit.isel(realization=ids)
[5]:
<xarray.Dataset> Size: 1kB
Dimensions: (horizon: 2, realization: 25)
Coordinates:
* horizon (horizon) <U9 72B '2041-2070' '2071-2100'
Dimensions without coordinates: realization
Data variables:
delta_annual_tavg (horizon, realization) float64 400B 3.6 4.468 ... 8.912
delta_annual_prtot (horizon, realization) float64 400B -1.739 ... 16.59
delta_JJA_prtot (horizon, realization) float64 400B -0.7181 ... 4.332With this reduced number, we can now compare the distribution of the selection versus the original ensemble of simulations.
[6]:
plt.style.use("seaborn-v0_8-dark")
fig = plt.figure(figsize=(11, 9))
ax = plt.axes(projection="3d")
for h in ds_crit.horizon:
ax.scatter(
ds_crit.sel(horizon=h, realization=ids).delta_annual_tavg,
ds_crit.sel(horizon=h, realization=ids).delta_annual_prtot,
ds_crit.sel(horizon=h, realization=ids).delta_JJA_prtot,
label=f"delta {h.values} - selected",
)
ax.set_xlabel("delta_annual_tavg (C)")
ax.set_ylabel("delta_annual_prtot (%)")
ax.set_zlabel("delta_JJA_prtot (%)")
plt.legend()
plt.show()
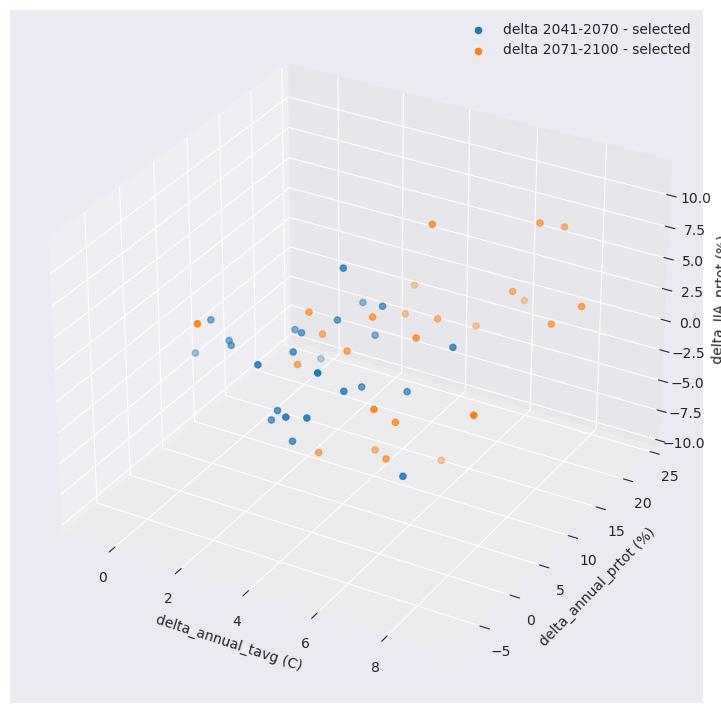
The function optionally produces a data dictionary for figure production of the associated R² profile.
The function ensembles.plot_rsqprofile provides plotting for evaluating the proportion of total variance in climate realizations that is covered by the selection.
In this case ~88% of the total variance in original ensemble is covered by the selection.
[7]:
ensembles.plot_rsqprofile(fig_data)
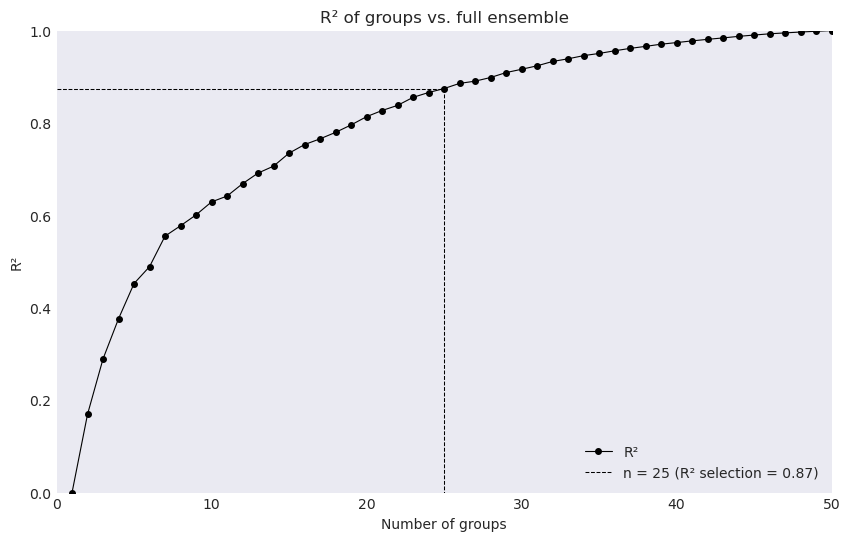
Alternatively, we can use method = {'rsq_cutoff':Float} or method = {'rsq_optimize':None} * For example, with rsq_cutoff we instead find the number of realizations needed to cover the provided \(R^{2}\) value
[8]:
ids1, cluster1, fig_data1 = ensembles.kmeans_reduce_ensemble(
data=crit, method={"rsq_cutoff": 0.75}, random_state=42, make_graph=True
)
ensembles.plot_rsqprofile(fig_data1)
ds_crit.isel(realization=ids1)
[8]:
<xarray.Dataset> Size: 840B
Dimensions: (horizon: 2, realization: 16)
Coordinates:
* horizon (horizon) <U9 72B '2041-2070' '2071-2100'
Dimensions without coordinates: realization
Data variables:
delta_annual_tavg (horizon, realization) float64 256B 5.646 3.6 ... 6.753
delta_annual_prtot (horizon, realization) float64 256B 14.42 ... 8.628
delta_JJA_prtot (horizon, realization) float64 256B -1.108 ... 6.548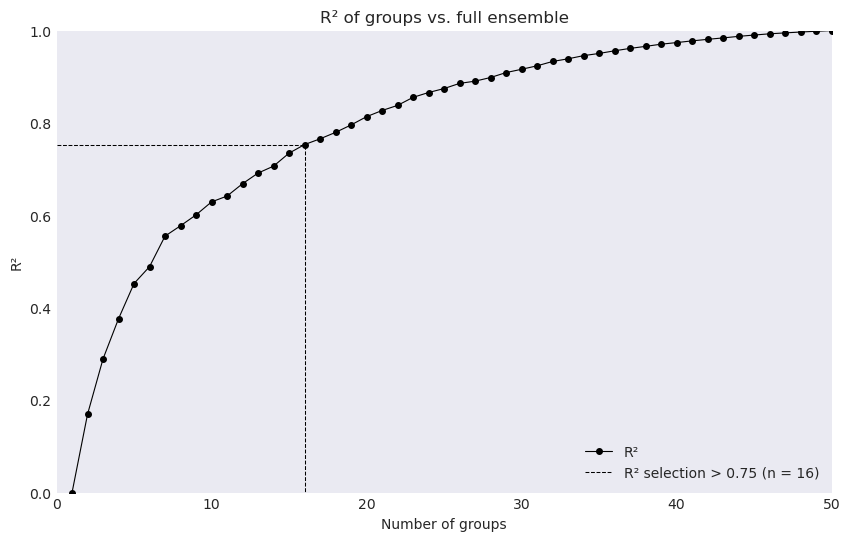
KKZ reduce ensemble
xclim also makes available a similar ensemble reduction algorithm, ensembles.kkz_reduce_ensemble. See: https://doi.org/10.1175/JCLI-D-14-00636.1
The advantage of this algorithm is largely that fewer realizations are needed in order to reach the same level of representative members than the K-means clustering algorithm, as the KKZ methods tends towards identifying members that fall towards the extremes of criteria values.
This technique also produces nested selection results, where an additional increase in desired selection size does not alter the previous choices, which is not the case for the K-means algorithm.
[9]:
ids = ensembles.kkz_reduce_ensemble(crit, num_select=10)
ds_crit.isel(realization=ids)
[9]:
<xarray.Dataset> Size: 552B
Dimensions: (horizon: 2, realization: 10)
Coordinates:
* horizon (horizon) <U9 72B '2041-2070' '2071-2100'
Dimensions without coordinates: realization
Data variables:
delta_annual_tavg (horizon, realization) float64 160B 1.719 ... 7.449
delta_annual_prtot (horizon, realization) float64 160B 9.611 ... 22.34
delta_JJA_prtot (horizon, realization) float64 160B -0.1268 ... 7.207[10]:
plt.style.use("seaborn-v0_8-dark")
fig = plt.figure(figsize=(9, 9))
ax = plt.axes(projection="3d")
for h in ds_crit.horizon:
ax.scatter(
ds_crit.sel(horizon=h, realization=ids).delta_annual_tavg,
ds_crit.sel(horizon=h, realization=ids).delta_annual_prtot,
ds_crit.sel(horizon=h, realization=ids).delta_JJA_prtot,
label=f"delta {h.values} - selected",
)
ax.set_xlabel("delta_annual_tavg (C)")
ax.set_ylabel("delta_annual_prtot (%)")
ax.set_zlabel("delta_JJA_prtot (%)")
plt.legend()
plt.show()
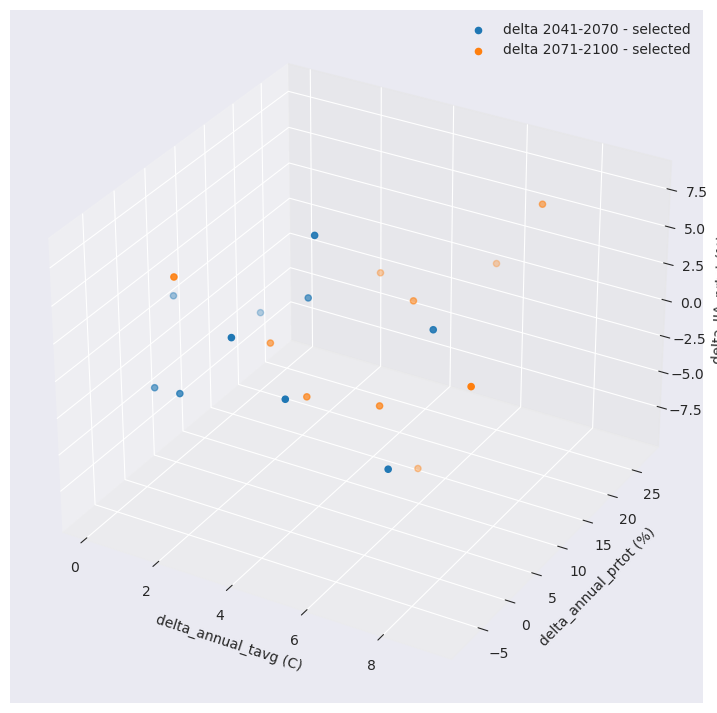
KKZ algorithm vs K-Means algorithm
To give a better sense of the differences between Nested (KKZ) and Unnested (K-Means) results, we can progressively identify members that would be chosen by each algorithm through an iterative fashion.
[11]:
## NESTED results using KKZ
for n in np.arange(5, 15, 3):
ids = ensembles.kkz_reduce_ensemble(crit, num_select=n)
print(ids)
[19, 24, 33, 3, 21]
[19, 24, 33, 3, 21, 18, 35, 48]
[19, 24, 33, 3, 21, 18, 35, 48, 40, 39, 29]
[19, 24, 33, 3, 21, 18, 35, 48, 40, 39, 29, 11, 2, 8]
[12]:
## UNNESTED results using k-means
for n in np.arange(5, 15, 3):
ids, cluster, fig_data = ensembles.kmeans_reduce_ensemble(
crit, method={"n_clusters": n}, random_state=42, make_graph=True
)
print(ids)
[7, 12, 27, 35, 45]
[12, 14, 19, 26, 27, 35, 45, 49]
[2, 12, 14, 16, 17, 22, 27, 38, 40, 45, 49]
[2, 12, 14, 16, 17, 19, 22, 27, 33, 39, 40, 42, 45, 49]
While the Nested feature of the KKZ results is typically advantageous, it can sometimes result in unbalanced coverage of the original ensemble. In general, careful consideration and validation of selection results is suggested when ``n`` is small, regardless of the technique used.
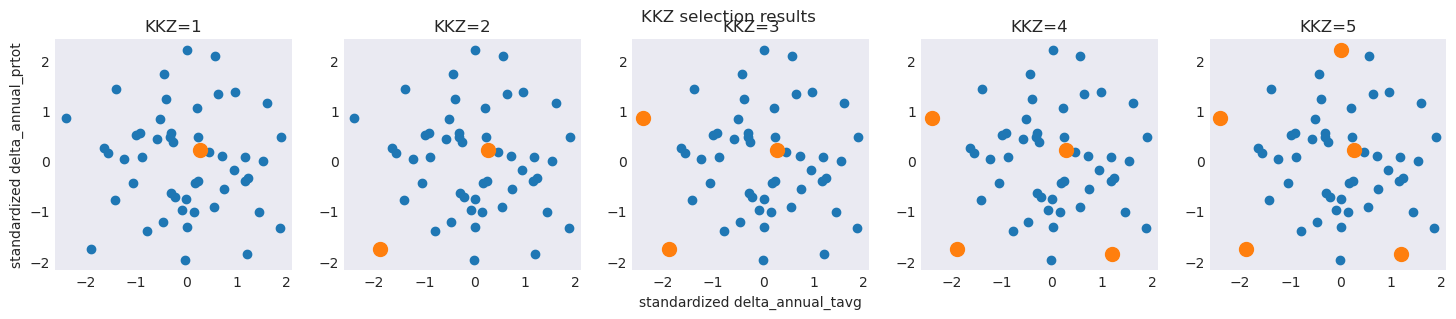
To illustrate, a simple example using only 2 of our criteria shows differences in results between the two techniques:
The KKZ algorithm iteratively maximizes distance from previous selected candidates - potentially resulting in ‘off-center’ results versus the original ensemble
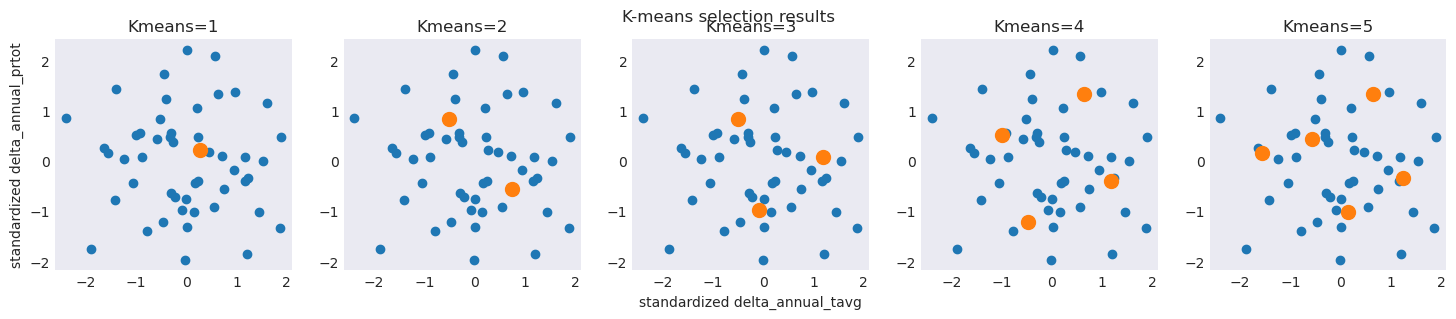
The K-means algorithm will redivide the data space with each iteration, producing results that are consistently centered on the original ensemble but lacking coverage in the extremes
[13]:
df = crit.isel(criteria=[0, 1])
# Use standardized data in the plot so that selection distances is better visualized
df = (df - df.mean("realization")) / df.std("realization")
plt.figure(figsize=(18, 3))
for n in np.arange(1, 6):
plt.subplot(1, 5, n, aspect="equal")
plt.scatter(df.isel(criteria=0), df.isel(criteria=1))
ids_KKZ = ensembles.kkz_reduce_ensemble(crit.isel(criteria=[0, 1]), num_select=n)
plt.scatter(
df.isel(criteria=0, realization=ids_KKZ),
df.isel(criteria=1, realization=ids_KKZ),
s=100,
)
plt.title(f"KKZ={n}")
if n == 1:
plt.ylabel("standardized delta_annual_prtot")
if n == 3:
plt.xlabel("standardized delta_annual_tavg")
plt.suptitle("KKZ selection results")
plt.figure(figsize=(18, 3))
for n in np.arange(1, 6):
plt.subplot(1, 5, n, aspect="equal")
plt.scatter(df.isel(criteria=0), df.isel(criteria=1))
ids_Kmeans, c, figdata = ensembles.kmeans_reduce_ensemble(
crit.isel(criteria=[0, 1]),
method={"n_clusters": n},
random_state=42,
make_graph=True,
)
plt.scatter(
df.isel(criteria=0, realization=ids_Kmeans),
df.isel(criteria=1, realization=ids_Kmeans),
s=100,
)
plt.title(f"Kmeans={n}")
if n == 1:
plt.ylabel("standardized delta_annual_prtot")
if n == 3:
plt.xlabel("standardized delta_annual_tavg")
plt.suptitle("K-means selection results")
plt.show()